ATP: The Great Carrier
Primary tabs
"ATP is the fuel of the cell." We have all heard this many times, but the reason why ATP (adenosine tri-phosphate) stores energy is not well understood. In essence, ATP is a standard activated carrier. It stores free energy only because the cell keeps $\conc{ATP}$ well above its equilibrium value.

The ATP/ADP equilibrium greatly favors ADP
ATP does not store free energy because of a "high energy phosphate bond" or because heat is released upon ATP hydrolysis - even though these descriptors themselves may be accurate. Rather, such details of the ATP molecule (which, presumably, are dominated by the proximity of like-charged phosphate groups) lead to an equilibrium which greatly favors ADP formation. That is, if both ATP and ADP are present in a solution, then after enough time very little ATP will remain. (How much time is 'enough' will depend on whether a catalyst is present.)

As with any activated carrier, to understand ATP we first examine the equilibrium point - which will serve as a reference point for understanding the non-equilibrium conditions prevailing in the cell. In equilibrium, the decomposition and synthesis of ATP will exactly balance.
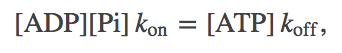 (1)
(1)where $\koff$ should be understood as an effective rate constant incorporating water's effects (see Exercises, below). In exact analogy with a binding analysis, we can re-write this as
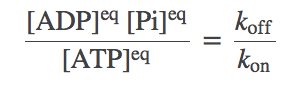 (2)
(2)ATP in the cell: The skewed equilibrium point makes ATP an effective carrier
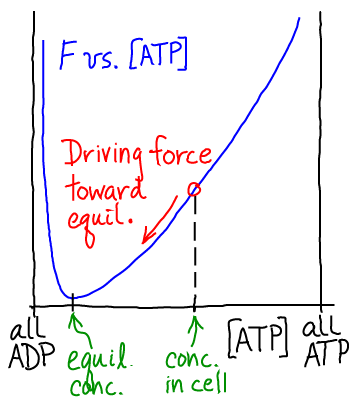
ATP is an ideal carrier because a lot of free energy is stored when both ADP and ATP are present in reasonable cellular concentrations. That is, at typical cellular concentrations $\cc{\cdots}$, we have
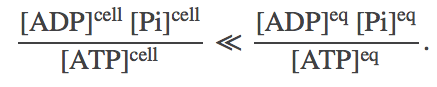 (3)
(3)As sketched above, this non-equilibrium condition creates a driving force toward equilibrium. The thermodynamics of this driving are most naturally quantified using the chemical potential.
The cell does not allow ATP and ADP to mutually equilibrate (i.e., reach the free energy minimum). Instead the cell is perpetually synthesizing new ATP from nutrients, creating a flow of free energy through the system in what we could call the big energy cycle of life.
Note that, as suggested in the sketch above, ADP could act as a carrier of free energy if it were maintained at sufficiently high concentration (beyond the equilibrium point, to the left in the sketch). Needless to say, the cell is not set up to use energy stored in ADP!
Kinetics and Catalysts
Like any carrier, ATP is "kinetically stable" - it is overwhelmingly decomposed by enzymatic catalysis because spontaneous hydrolysis in solution is very slow compared to cellular processes. Thus, ATP fulfills the necessary criteria for a carrier: (1) it is maintained out of equilibrium, and (2) it only decomposes enzymatically as part of cellular processes: transport, phosphorylation, and myriad other tasks.
Appreciating ATP as an ordinary activated carrier enables us to re-envision molecular motors as simple enzymes that happen to couple catalysis to translation. You can consider a thought experiment studying motor motion near the ADP/ATP equilibrium.
References
- J. M. Berg et al., "Biochemistry", W. H. Freeman. The 2002 edition is online for free.
- B. Alberts et al., "Molecular Biology of the Cell", Garland Science (many editions available). The 2nd chapter has an oustanding discussion of energy use. Consider it required reading.
- R. Phillips et al., "Physical Biology of the Cell," (Garland Science, 2009).
- Any bioenergetics book will give basic information about ATP as a carrier. Examples are
- D. G. Nicholls et al., "Bioenergetics", Academic Press. A standard text.
- D. A. Harris, "Bioenergetics at a glance", Wiley-Blackwell. Concise, clear, and a favorite of mine.
Exercises
- The full chemical equation for ATP hydrolysis of course includes water. Explain why a mass-action description including water's concentration would be inappropriate by considering the limitations described for mass action.
