ATP and Other Activated Carriers
Primary tabs
Activated Carriers: Why chemical energy storage is "statistical"
Any system that is out of equilibrium stores free energy. The cell stores free energy using out-of-equilibrium chemically reacting systems involving molecules known as "activated carriers," as well as non-equilibrium concentration differences - gradients - across membranes.
Activated carriers are molecules that can be split (C $\rightarrow$ A + B) to release free energy but only if there is an excess of C relative to its equilibrium concnetration. Key examples are ATP, GTP, NADH, FADH$_2$, and NADPH. GTP is used as a free energy source to reduce errors in translation in a process called "kinetic proofreading".
In order for carriers like ATP to be a stable source of free energy, they must stay "activated" when not being used for cellular purposes. In other words, the decomposition/splitting reaction C $\rightarrow$ A + B must be slow compared to cellular timescales and unlikely to occur without catalysis.
For completeness, we emphasize that free energy is stored because the decompostion/synthesis reactions are maintained away from equilibrium - not because bond-breakage is involved. Free energy could equally well be stored in an isomerization "reaction" $A \rightleftharpoons A'$, in which the species populations were maintained away from equilibrium.
The physical basis of carrier activation
Understanding activated carriers begins with the reversible equation for a decomposition reaction

where "C" could be any carrier such as ATP. We have used the rates $\kon$ and $\koff$ both because these have the corrects units (see notation) and also to suggest that details of the chemical reaction are not important. Conceptually, we can understanding the equilibrium (or lack of it) in a chemical reaction in the same way as we understand binding.
Using a mass-action picture, equilibrium occurs when the number of reactions occuring per second in the forward direction, $\conc{A} \conc{B} \, \kon$, balances the number in the reverse direction, $\conc{C} \, \koff$. That is, equilibrium occurs when
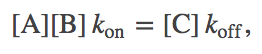 (1)
(1)and thus a carrier C is activated whenver the concentrations are such that
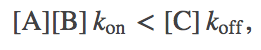 (2)
(2)meaning that more decomposition than synthesis events occur per second.
Pictorially, the conditions of equilibrium and out-of-equilibrium activation are shown below.

Note that the system could be out of equilibrium in the opposite way - with an excess of "B" (e.g., ADP) relative to its equilibrium value - which would also store free energy.
A non-equilibrium condition - one not satisfying (1) - stores free energy because there is a tendency for the system to relax back to equilibrium. In the case of a carrier, there is a (strong) tendency for the system to decompose, and this will lead to net flow in one direction in biochemical cycles using the carrier. The tendency is strong because the cell maintains carrier concentrations far from equilibrium.
Other carriers
The physical explanation just given suggests that ATP is not the only molecule that can be used as an activated carrier. Indeed, it is well known that GTP is used as a carrier for signaling processes and for translation. The logic here also explains energy storage in electron carriers like NADH, which participate in the oxidative phosphorylation process that "activates" ATP in the first place by synthesizing it well beyond its equilibrium value.
A Simple, Quantitative Model for Free Energy Storage in Activated Carriers
We can use the same approach taken to analyze binding to see how free energy is stored in a very simple model. In particular, we can model the A, B, and C components (e.g., ADP, Pi, and ATP) as non-interacting except for their probilities to react or decompose. This is nothing other than a mass-action picture - or, thermodynamically, treatment of the components as ideal gases.
We treat the reaction $A + B \rightleftharpoons C$, as involving ideal gases of $\na$ A molecules, $\nb$ B molecules, and $\nc$ C molecules. We assume there is a (free) energy change of $\dmu$ for every C molecule synthesized. See the binding discussion for details. These assumptions lead to a total free energy of the system given by
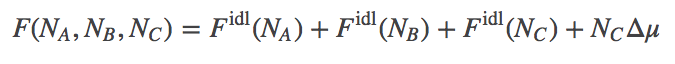 (3)
(3)Based on Eq. (3) and the function $\fidl$, we can solve for the equilibrium point - the most probable state when $N$ values are large - and we find
 (4)
(4)Any concentrations that do not satisfy the relation given in Eq. (4) are out of equilibrium and hence store free energy.
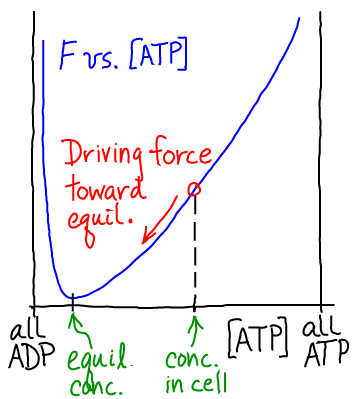
In the case of $\mbox{ADP} + \mbox{Pi} \rightleftharpoons \mbox{ATP}$, as sketched in the figure, the equilibrium point greatly favors low ATP (high ADP) concentration. However, the cell maintains $\conc{ATP}$ much higher than its equilibrium value. Thus a driving force for hydrolysis of ATP is always present, like electricity in wall outlets. Again, ATP is a source of energy only because it is maintained out of equilibrium with its hydrolysis product ADP. If $\conc{ATP}$ were allowed to reach its equlibrium value, no free energy would be stored. From a microscopic point of view, at equilibrium, hydrolysis reactions would exactly be balanced by synthesis; reverse processes would balance forward processes.
References
- B. Alberts et al., "Molecular Biology of the Cell", Garland Science (many editions available). The 2nd chapter has an oustanding discussion of energy use. Consider it required reading.
- Any bioenergetics book will give basic information about ATP as a carrier. Examples are
- D. G. Nicholls et al., "Bioenergetics", Academic Press. A standard text.
- D. A. Harris, "Bioenergetics at a glance", Wiley-Blackwell. Concise, clear, and a favorite of mine.
